Berikut ini penjelasan mengenai Barisan Dan Deret Geometri beserta soal dan pembahasannya setelah sebelumnya kita membahasa barisan dan deret aritmatika. Jika Anda bisa memperhatikan dengan benar, materi SMP kelas 8 dan 9 ini cukup mudah.
Perhatikan ulasan berikut untuk menambah pemahaman Anda mengenai barisan dan deret geometri.
Konten
Baris Geometri
Baris Geometri adalah barisan yang mempunyai perbandingan tetap pada setiap dua suku yang berurutan Perbedaan dengan barisan aritmatika yaitu barisan aritmatika memiliki pertambahan dan pengurangan yang tetap, sedangkan barisan geometri memiliki perbandingan tetap berupa perkalian atau pembagian.
Rumus Baris Geometri
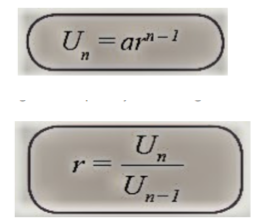
Un = Suku ke n
Un-1 = Suku ke n – 1
r = Rasio
a = Suku pertama
Contoh Baris Geometri
3, 6, 12, 24, 48, 96, … dan seterusnya
1, 3, 9, 27, 81, 243, … dan seterusnya
2, 6, 18, 54, 162, 486, … dan seterusnya
Jika Anda memperhatikan contoh baris geometri diatas, perbandingan dari barisan yang berurutan tetap.
6 = 12 = 24 = 48 = 96 = 2
3 6 12 24 48
3 = 9 =27 = 81 = 243 = 3
1 3 9 27 81
6 = 18 = 54 = 162 = 486 = 3
2 6 18 54 162
Contoh Soal Dan Pembahasan Baris Geometri
Soal 1: Tentukan suku ke 11 dari barisan geometri 3, 9, 27, 81, …
Jawab :
a = 3
r = Un / Un-1
= 9 / 3
= 3
Un = arn-1
U11 = 3 . 3 11- 1
= 3 . 3 10
= 3. 59049
= 177.147
Jadi suku ke 11 dari barisan geometri tersebut yaitu 177.147
Soal 2: Diketahui barisan geometri 1, 4, 16, 64, … Tentukan suku ke 7 dari barisan geometri tersebut
Jawab :
a = 1
r = Un / Un-1
= 4 / 1
= 4
Un = arn-1
U11 = 1 . 4 7- 1
= 1 . 4 6
= 1 . 4096
= 4.096
Jadi suku ke 7 dari barisan geometri tersebut yaitu 4.096
Soal 3: Tentukan rasio dan suku ke 6 dari barisan deret geometri 2, 8, 32, 148, …
Jawab :
r = Un/ Un-1
= 8 / 2
= 4
U6 = 2 . 4 6- 1
= 2 . 4 5
= 2. 1204
= 2.048
Jadi rasio dari barisan geometri adalah 4 dan suku keenam adalah 2.048.
Deret Geometri
Deret Geometri sama halnya dengan deret aritmatika, perbedaannya yaitu deret geometri dengan perbandingan perkalian atau pembagian, sedangkan aritmatika dengan pertambahan atau pengurangan.
Deret Geometri Adalah jumlah suku dari barisan geometri yang mempunyai perbandingan atau rasio yang tetap.
Contoh Deret Geometri
2, 6, 12, 24, 48, 96, …, Un
Maka deret Geometri yaitu :
2 + 6 + 12 + 48 + 96 + …+ Un
1, 5, 25, 125, 625, …, Un
Maka deret Geometri yaitu :
1 + 5 + 25 + 125 + 625 + …+ Un
Rumus Deret Geometri

Sn = Jumlah suku ke n
r = Rasio
a = Suku pertama
Deret Geometri Tak Hingga terbagi menjadi dua jenis yaitu tak hingga divergen dan tak hingga konvergen. Deret Geometri tak hingga divergen adalah deret geometri yang nilai bilangannya semakin membesar hingga tidak dapat dihitung lagi.
Sedangkan Deret Geometri Tak Hingga Konvergen adalah deret geometri yang bilangannya semakin mengecil dan dapat dihitung jumlahnya.
Tak Hingga Divergen
Contoh deret Geometri Tak Hingga Divergen
2, 6, 12, 24, 48, 96, 192, 384, ….
Jika diteruskan maka jumlah seluruhnya tidak bisa dihitung karena semakin besar.
Tak Hingga Konvergen
Contoh Deret Geometri Tak Hingga Konvergen
96, 48, 24, 12, 6, 2, 2/3, 2/ 9, 2/ 18, ….
Jika diteruskan maka nilai dari deret geometri semakin mengecil dan ujungnya mendekati 0.
Contoh Soal Dan Pembahasan Deret Geometri
Soal 1: Diketahui barisan geometri memiliki suku pertama atau a yaitu 8 dan rasio 2. Tuliskan barisan dan deret geometri
Jawab :
Barisan Geometri yaitu 8, 16, 32, 64, 128, 256, …, Un
Deret Geometri yaitu 8 + 16 + 3 + 64 + 128 + 256 + … + Un
Soal2: Tentukan jumlah 7 suku pertama dari barisan 2, 4, 6, 8, …
Jawab :
a = 2
r = Un / Un-1
= 4 / 2
= 2
Sn = a ( rn – 1 ) / ( r – 1 )
S7 = 2 ( 27 – 1 ) / (2 – 1)
= 2 ( 128- 1 ) / 1
= 2 . 127
= 254
Demikian sedikit ulasan mengenai Barisan Dan Deret Geometri beserta soal dan pembahasanya. Kunci dari barisan dan deret Geometri yaitu Anda harus pintar atau mahir dalam pembagian dan pertambahan. Tidak lupa Anda memahami dan menghafal rumus-rumus dari barisan dan deret geometri tersebut.
Sumber:
- https://www.blogteknisi.com/2018/04/rumus-barisan-geometri-dan-contoh-soalnya.html
- http://isengnulis.com/penjelasan-dan-rumus-deret-geometri-serta-contoh-soal-deret-geometri/
Originally posted 2019-09-12 09:14:04.


Min itu yang rumus sn bukannya 7-1 dulu ya abis itu baru dipangkatkan?
Itu ga dikurang 1 dlu karena 1 nya setara sama bilangan 128 bukan diatas/dipangkat
@Bam
Di ketahui barisan bilangan 1/4, 1/2, 1, 2, 4…. tentukan suku ke 11 barisan tersebut!