Barisan dan Deret Aritmatika merupakan salah satu materi matematika tingkat SMP kelas 8. Berikut ini penjelasan lengkap mengenai barisan dan deret aritmatika. Baik pengertian, rumus, contoh, soal dan pembahasannya. Simak dan pahami ulasan berikut ini.
Konten
Barisan Aritmatika
Barisan dan Deret Aritmatika merupakan baris bilangan yang berdasarkan pola. Baris Aritmatika Adalah adalah barisan bilangan yang memiliki selisih atau beda antara dua suku barisan yang berurutan.
1 5 9 13 17 21 25 29
Barisan berurutan tersebut memiliki selisih atau beda 4 antara dua suku barisan yang berurutan. Hal tersebut membuktikan bahwa baris bilangan diatas merupakan barisan aritmatika. Barisan aritmatika memiliki beda yang tetap dimana sering dilambangkan dengan “b”.
Jika beda “b” bernilai positif, maka barisan arimatika dikatakan barisan aritmatika naik. Jika beda “b” bernilai negatif, maka barisan aritmatika tersebut dikatakan barisan aritmatika turun. Ciri-cici dari barisan aritmatika yaitu memiliki beda yang sama dari satu bilangan ke bilangan berikutnya.
Rumus Baris Aritmatika
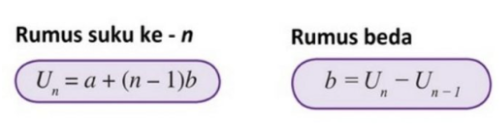
Keterangan :
Un = Suku ke n
a = Suku pertama
b = Beda
Un-1= Suku sebelum n
Contoh Baris Aritmatika
3, 5, 7, 9, 11, 13, 15, 17, 19, … dan seterusnya
1, 4, 7, 10, 13, 16, 19, 21, … dan seterusnya
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … dan seterusnya
Contoh Soal Dan Pembahasan Baris Aritmatika
Soal 1
Diketahui barisan aritmatika sebagai berikut
7, 10, 13, 16, 19, 21, …
Tentukan :
- Beda
- Jenis barisan aritmatika
- Suku ke sebelas barisan tersebut
Jawab 1:
b = U2 –U1
= 10 – 7
= 3
Jawab 2:
beda lebih dari 0 b > 0, maka barisan aritmatika tersebut merupakan barisan aritmatika naik.
Jawab 3:
Un = a + (n – 1) b
U11 = 7 + (11- 1) 3
= 7 + 10 . 3
= 7 + 30
= 37
Jadi suku ke sebelas dari barisan tersebut adalah 37
Soal 2
Sebuah barisan aritmatika memiliki suku pertama 6 dan suku ke delapan 41.
- Tentukan beda pada barisan aritmatika tersebut
- Tuliskan sepuluh suku pertama pada barisan aritmatika tersebut.
Jawab 1:
Menentukan beda :
a = 6
U8= 41
Un = a + ( n – 1 )b
U8 = 6 + ( 8 – 1 )b
41 = 6 + 7.b
41 = 6 + 7b
41 – 6 = 7b
35 = 7b
b = 35 : 7
b = 5
Jadi, beda pada barisan aritmatika tersebut adalah 5
Jawab 2:
Dengan suku pertama 6 dan beda 5, maka diperoleh barisan aritmatika sebagai berikut
6, 11, 16, 21, 26, 31, 36, 41, 46, 51
Soal 3
Tentukan suku ke 11 dari barisan aritmatika 3, 7, 11, 15, ….
Jawab :
b = U2 –U1
= 7 – 3
= 4
Un = a + ( n – 1) b
U11 = 3 + ( 11- 1) 4
= 3 + 10 . 4
= 3 + 40
= 43
Jadi suku kesebelas dari barisan aritmatika tersebut adallah 43.
Deret Aritmatika
Deret Aritmatika adalah jumlah suku ke n pada barisan aritmatika. Deret aritmatika merupakan pembahsan mengenai jumlah suku – suku berurutan tersebut.
Rumus Deret Aritmatika
Un = Suku ke n
a = Suku pertama
b = Beda
Sn = Jumlah suku ke n
Contoh Deret Aritmatika
Contoh Deret Aritmatika bentuk umum yaitu :
U1+ U2+ U3+ U4+ U5+ U6+ U7+ … + Un
2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + … + Un
6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + … + Un
Contoh Soal Dan Pembahasan Deret Aritmatika
Soal 1:
Jumlah 10 suku pertama dari deret aritmatika 5, 7, 9, 11, 13, 15, …. adalah
Jawab :
a = 3
b = U2 – U1
= 7 – 5
= 2
Un = n / 2 ( 2a + ( n-1 ) b)
U10 = 10 / 2 ( 2.5 + (10 – 1 ) 2)
= 5 ( 10 + 9 .2 )
= 5 ( 10 + 18 )
= 5 ( 28 )
= 140
Soal 2:
Tentukan jumlah 12 suku pertama dari deret aritmatika 3, 6, 9, 12, 15, 18, 21, …
Jawab :
a = 3
b = U2 – U1
= 6 – 3
= 3
Un = n / 2 ( 2a + ( n-1 ) b)
U12 = 12 / 2 ( 2.3 + (12 – 1 ) 3)
= 6 ( 6 + 11 .3 )
= 6 ( 6 + 33)
= 6 ( 39 )
= 234
Demikian penjelasan mengenai Barisan dan Deret Aritmatika yang meliputi pengertian, rumus, contoh, soal dan pembahasannya. Selanjutnya kita juga akan belajar mengenai barisan dan deret geometri. Semoga penjelasan tersebut bermanfaat dan memudahkan Anda dalam mengerjakan soal.
sumber: https://rumus.co.id/deret-aritmatika/
Originally posted 2019-09-12 13:12:24.



Suatu barisan bilangan mempunyai rumus suku ke-n,Un=28-3n.Nilai suku ke-36 adalah…
a. -80
b. -75
c. -70
d. -65
hayooo berapa?
Diket :
Un = 28 – 3n
U36 = 28 – 3 (36)
U36 = 28 – 108
U36 = -80
A. -80
Un= 28-3n
U36= 28-3(36)
= 28-108
= -80
Un=28-3n
N=36
Un=28-3n
U36=28-(3×36)
U36=28-108
U36=-80